One of the most fascinating things about mathematics is the way it seems so presciently adapted to enabling physicists to speak about nature. And not just to speak, but to understand, and to discover new aspects of reality and invent new models and technologies.
Of course, “pure” mathematicians love the mathematical language just for its own sake – after all, it’s a sublime creation of the human mind. On the other hand, “applied” mathematicians tend to have a foot in both camps: they love an elegant proof as much as any pure mathematician does, but they also get a thrill when their mathematics helps shed light on physical reality. And a key way it does this is through analogies.
A particularly intriguing analogy is that between Albert Einstein’s equations of gravity and James Clerk Maxwell’s equations of electromagnetism. It’s led to an exciting field of research called “gravitoelectromagnetism” – and to the prediction of a new force, “gravito-magnetism”. The idea of such a force is surely unimaginable without the help of a mathematical or physical analogy, but astonishingly, recent evidence suggests that it really exists.
But first let me clarify the term “mathematical analogy”. In its strictest form, it means that the equations describing two different things look similar. A classic 18th century example is Isaac Newton’s law of gravity, and Charles Augustin de Coulomb’s law of electrostatics. Both have the same “inverse-square” form, kab/r² , where r is the distance between two objects A and B. In Newton’s law, a and b are the masses of two objects, while in Coulomb’s law they are the electric charges. (The constant k is also different in each case, and depends on the units of measurement.)
Fast-forward a century to 1865, and James Clerk Maxwell’s mathematical formulation of the laws of electromagnetism – the equations that show how changing (non-static) electric currents can create magnetism, and how moving magnets create electricity.
This extraordinary interconnection – called electromagnetic induction – was discovered experimentally by Hans Oersted and Michael Faraday, and put into full mathematical form by Maxwell. It’s the same induction now familiar in induction cooktops, and which is the secret of other electromagnetic technologies such as electric motors and electricity generators.
And it’s this same induction that would prove foundational for the concept of gravito-electromagnetism. It’s all about language. Maxwell wrote profoundly on the importance, and the pitfalls, of drawing conclusions from analogies – and he used them brilliantly in formulating his famous equations.
First, inspired by the intuitive ideas of Faraday, he created the concept of the mathematical field in physics. The idea is that you can assign a mathematical value to a physical quantity, such as electromagnetic force, at every point in space – just as a field of wheat is made up of each individual plant. It was a radical idea 150 years ago, because it was widely assumed that electromagnetic and gravitational forces acted instantaneously, rather than needing time and space for their propagation.
The $64,000 question has long been: how far can such mathematical analogies be pushed?
Next, he discovered one of the most compelling mathematical analogies in the history of physics – that between the known equation describing the way a wave travels along a plucked guitar string, and a pair of equations he deduced from his mathematical electromagnetic field. Just as with Newton’s and Coulomb’s inverse-square laws, the analogy here showed up as a similar pattern in the form of the equations – except that unlike the vibrating guitar string, the electromagnetic waves travelled with the speed of light.
This was such an amazing coincidence that Maxwell made a bold prediction: not only does electromagnetism travel as a wave of oscillating electric and magnetic fields, but light itself is as an electromagnetic wave. Two long-standing physics puzzles solved via one mathematical analogy: no instantaneous electromagnetic action-at-a-distance, and the nature of light uncovered! (Thomas Young had identified the wave motion of light in 1801, but no-one had known what it was made of – what it was that was “waving” or oscillating.)
Fast forward now to 1916, by which time Einstein had adapted Maxwell’s field idea in order to update Newton’s theory of gravity, which he incorporated into the general theory of relativity (GR).
Einstein’s adaptation of the mathematical field concept from one theory to another illustrates a different way in which mathematical analogies can be fruitful in physics. Maxwell’s was a vector field, and Einstein utilised tensor fields. Tensors are generalised analogies of vectors. (And here’s a grateful nod to the pure mathematicians – vectors, tensors, and many more such powerful concepts began life as purely mathematical curiosities.)
Vectors can be usefully imagined as arrows, whose length and direction represent two different attributes, such as the strength and direction of a force. Tensors can represent any number of quantities, so they can be used to describe more complex phenomena – such as Einstein’s gravitationally curving 4D space-time.
Maxwell, Faraday and Einstein had all suspected there were mathematical or physical analogies between electromagnetism and gravity, and it turns out that there are several. Two, in particular, have attracted a great deal of attention from mathematicians.
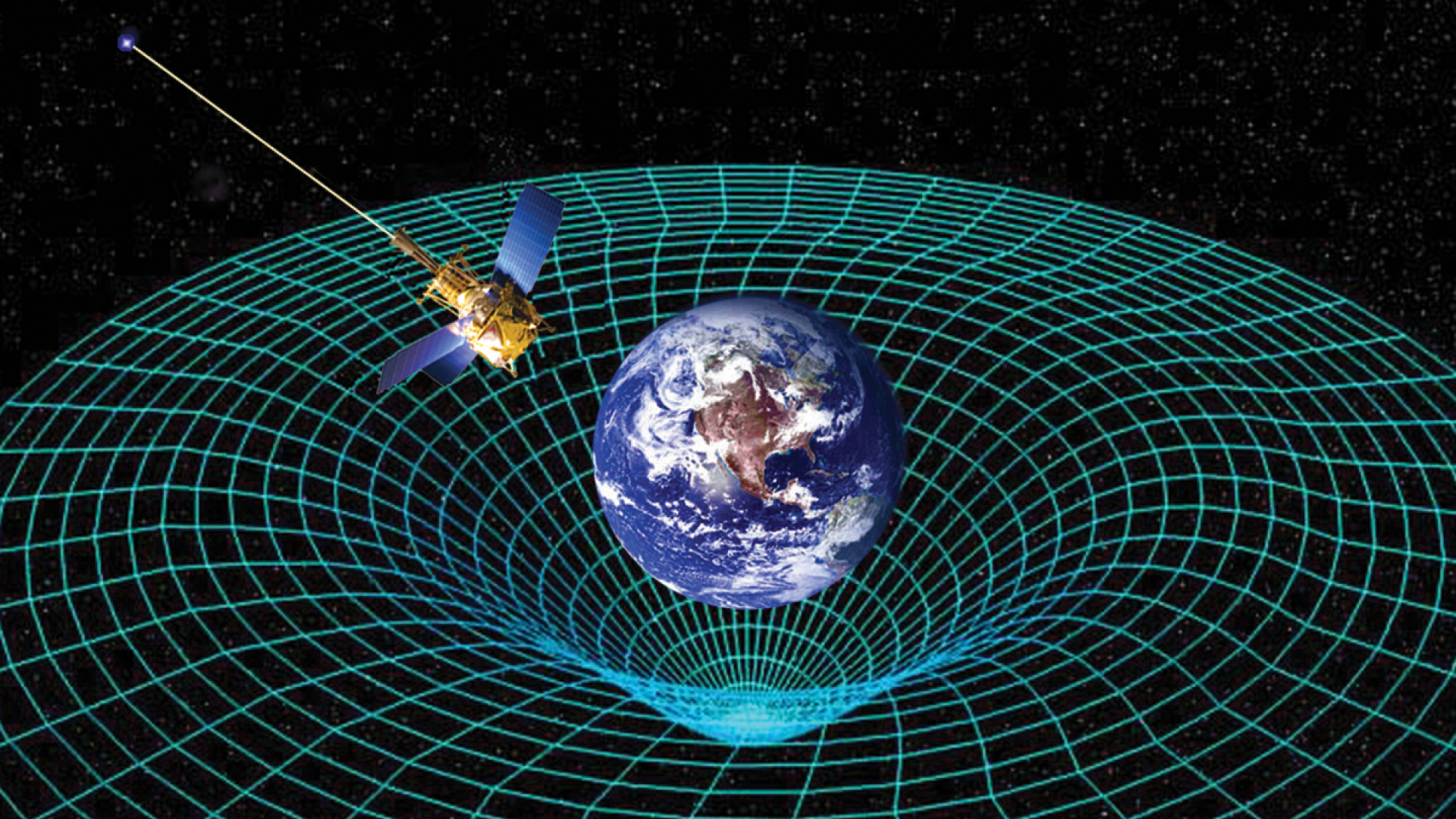
The first one, initially explored by Einstein in 1913 and by Josef Lense and Hans Thirring in 1918, includes the gravitational analogue of electromagnetic induction. Today this so-called “gravito-electromagnetism”, or GEM for short, is generally treated mathematically via the “weak field” or “linearised” approximation to the full GR field equations – simpler versions that work well in weak fields such as that of the Earth.
To explain this a little more, the point of solving Einstein’s equations is to find a gravitational field’s space-time metric – the rule for measuring distances in curved space-time, analogous to Pythagoras’s theorem as the rule for the length of a line in flat 2 or 3D (“Euclidean”) space. A weak-field metric is essentially that of flat 4D (“Minkowski”) space-time – which is space-time in regions far away from the effects of matter – plus a small additional term encoding the curvature caused by the weakly gravitating matter. But here’s the amazing thing: this additional term also yields quantities satisfying equations that look remarkably similar to Maxwell’s. The “gravitoelectric” part can be readily identified with the everyday Newtonian downward force that keeps us anchored to the Earth. The “gravito-magnetic” part, however, is something entirely unfamiliar – a new force apparently due to the rotation of the Earth (or any large mass).
It’s analogous to the way a spinning electron produces a magnetic field via electromagnetic induction, except that a massive spinning object mathematically “induces” a “dragging” of space-time itself – as if space-time were like a viscous fluid that’s partially dragged around a rotating ball.
The $64,000 question has long been: how far can such mathematical analogies be pushed?
Is “gravito-magnetic induction” real? If it is, it should show up as a tiny wobble in the orbit of satellites and – thanks also to the “geodetic” effect, the curving of space-time by matter – as a change in the direction of the axis of an orbiting gyroscope. (The latter is analogous to the way a magnetic field generated by an electric current changes the orientation of a magnetic dipole.)
Finally, after a century of speculation, answers are unfolding. Independent results from several satellite missions – notably Gravity Probe B, LAGEOS, LARES, and GRACE – have confirmed the Earth’s geodetic and frame-dragging effects to varying degrees of precision. For frame-dragging, the best agreement with GR has been within 0.2%, with an accuracy of 5%, but astronomers expect that a new satellite (LARES 2), to be launched at the end of 2019, will, with data from LAGEOS, give an accuracy of 0.2%.
More accurate results will provide more stringent tests of GR, but astrophysicists have already taken gravito-magnetism on board. For instance, it suggests a mechanism to explain the mysterious jets of gas that have been observed spewing out of quasars and active galactic nuclei. Rotating supermassive black holes at the heart of these cosmic powerhouses would produce enormous frame-dragging and geodetic effects. A resulting gravito-magnetic field analogous to the magnetic field surrounding the two poles of a magnet would explain the alignment of the jets with the source’s north-south axis of rotation.
Making analogies is a tricky business, however, and from the mathematical point of view there are some interpretive anomalies still to unravel. Which leads to the second analogy between Einstein’s and Maxwell’s equations. Unlike the GEM analogy, this one arose in a purely mathematical context, pioneered by A. Matte in 1953.
Maxwell’s equations can be expressed in tensor form, by combining the electric and magnetic field vectors into a single tensor, called the Faraday tensor (or its “dual”, the Maxwell tensor). The relevant tensors in GR are the Riemann and Weyl. The first is defined in terms of derivatives of the metric tensor, so it describes the way gravity curves space-time. The Weyl tensor is the part of the Riemann tensor that describes the curvature only outside the gravitational source. In other words, it describes non-local gravitational effects, so it’s important in analysing gravitational radiation, and the evolution of the universe.
It turns out that just as the Faraday and Maxwell tensors can, in reverse, be split back into their electric and magnetic parts, so the Riemann and Weyl tensors can be split, in a formally analogous way, into “electric” and “magnetic” parts.
Einstein’s equations are notoriously difficult to solve, and these “electric” and “magnetic” tensors have proved useful in analysing particular classes of solutions. Many of these explorations have centred on intriguing mathematical challenges that are fascinating in their own right. But there’s also the exciting possibility that they will give new insight into the physics too – particularly cosmology and gravitational waves.
As for the relationship between these mathematical “electric” and “magnetic” tensors and the mathematical-physical GEM fields – the jury is still out. There’s still plenty left in the Maxwell-Einstein analogies to keep mathematicians engaged for a long time to come.
Login or Sign up for FREE to download the educational resources
This article was written by Robyn Arianhod, senior adjunct research fellow at the School of Mathematical Sciences at Monash University for COSMOS Magazine Issue 84.
COSMOS Magazine is Australia’s only dedicated print science publication. Subscribe here to get your quarterly fill of the best Science of Everything, from the chemistry of fireworks to cutting-edge Australian innovation.
MYCOSMOS for Teachers – Use you complimentary membership to access the full COSMOS Magazine digital collection.